これであなたの血液もサラサラ.

唐突な記録だが,今回の記録では2次函数のグラフを描く.

二次函数とは. ナントカの2乗って形の式のこと. ここでは$ y = x^2 $を使う. xが2乗になってるからちゃんとした2次函数. で,今回の記録は前述の通り,この$ y = x^2 $をグラフにするのだが,グラフは2次元のものを使う. 縦にyが伸びてて,横にxが広がってるグラフね.

グラフを出力↓

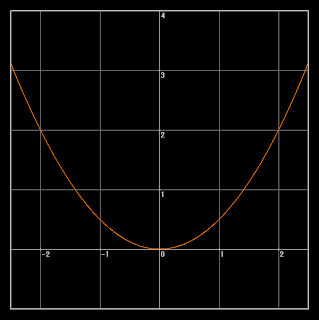
まずは$ y = x^2 $を描画.

この形が基本.

次に$ x^2 $を半分にしてみる.

$ x^2 $をもう少し割ってみる.
ということで３で割る.

このように,$ x^2 $は割れば割るほど
曲がりは外へと広がってゆく.

ということは,
逆に$ x^2 $を倍にすれば,
曲線は内側につぼまってゆくはず.

２倍してみる.

更に倍に,

１０倍

狭い. 細い.

ここであることに気が付く.
今までのグラフを,
全部まとめると,
あれに見えることに.

クリックで確認！

ただこれが言いたかった.
というか昔誰かがおっしゃっていた.



メメントモリ

126781159581673931 https://www.storange.jp/2013/05/blog-post_24.html https://www.storange.jp/2013/05/blog-post_24.html これであなたの血液もサラサラ. 2013-05-24T21:52:00+09:00 https://www.storange.jp/2013/05/blog-post_24.html Hideyuki Tabata Hideyuki Tabata 200 200 72 72